热力学与统计物理-1 导论
讲述了热力学和统计物理的关系,整个故事的脉络
导言
杂乱无章是我对《热学》这门课的唯一印象。$ P, V, T, N, U, H, S, F, G $都是状态参量,有些又叫做态函数。这么多状态参量,哪些是独立的?求出多少才到头?还有$ C_V, C_p, \kappa, \alpha, \beta$等一堆实验量究竟有什么作用?我相信这是许多同学学完热学后的感受。
在《热力学与统计物理》这门课,我们首先需要在热力学部分厘清这些概念。在看到经典热力学过分依赖实验的局限性后,学习统计力学通过等概率原理将微观量与宏观量联系起来的思路,理解热力学与统计物理的关系。
我的参考教材主要是Herbert B. Callen的Thermodynamics and statistical mechanics1、汪志诚先生的热力学与统计物理2以及北京师范大学晏世伟教授的自编教材。前两本教材点击链接下载即可。
热力学
热力学的基本概念由三大部分组成:物态方程、热力学基本定律和特性函数。热力学的核心问题是:在移动一个封闭的复合系统的内部限制之后,确定系统最终演化到的平衡态1。问就是求平衡态。有了这些基本概念,我们才能玩儿一些诸如相变之类的花招儿。
物态方程
热力学中的物态方程必须由实验测得。实验中经常通过计算体膨胀系数$ \alpha = \frac{1}{V} \left(\frac{\partial V}{\partial T}\right)_p $和等温压缩系数$ \kappa = - \frac{1}{V}\left(\frac{\partial V}{\partial p}\right)_V $,间接得到物态方程$ f(p, V, T) = 0 $。选择$\alpha,\kappa$的原因是等温和等压这两个条件比较好获得。
热力学基本定律
除了我们熟知的热力学第一定律$dU = \dbar Q + \dbar W$之外,热力学定律只能回答一些“模糊”的问题。第零定律告诉我们热平衡时温度相同,第二定律告诉我们系统向熵最大的方向演进,第三定律告诉我们绝对熵存在。好在后来的物理学家们给出了准确的数学表达,不过那已经是非常后面的事情了。在热力学发展的早期,这些定律确实显得模糊,远不像开普勒定律、库仑定律之类的实验定律一样“数学化”。
特性函数
熵表象与内能表象
随着熵的概念被提出,人们发现热力学系统朝着熵最大的方向演化,即热力学是有方向的。我们还知道,系统会朝着内能最小的方向演化。这样就构成了两种表象:熵表象和内能表象,分别对应两种基本方程3。这两种表象就像直角坐标系和球坐标系,求解问题时选一个就行,没有孰优孰劣之分。这是最重要的概念:对于一个系统,我们只关心熵或内能就足够了,其余的量均可以通过熵或内能推导出来。
内能表象下的基本方程为$U = U(S,V)$,S和V作为系统的独立变量,同时S和V还是内能的自然变量(natural variables)。U当然可以是其他独立变量,比如T和p的函数,但是选择S和V是最最最最最方便直观的。U的微分为$dU = TdS - pdV$,这说明在确定$U(S,V)$之后,$T = \left(\frac{\partial U}{\partial S}\right)_V$, $p = - \left(\frac{\partial U}{\partial V}\right)_S$可以直接求出来。
广延量与强度量
$dU = TdS - pdV$表明,$(T,S), (p,V)$是一对共轭变量。观察$(p,V)$:压强$p$的特点是与系统包含的粒子数无关,将两个相同的系统合并在一起,压强不变;体积$V$则与系统大小有关系了,将两个相同的系统合并在一起,体积是翻倍的。
若系统的某个物理量等于每个子系统的该物理量之和,则这个物理量称为广延量 (extensive parameters),强度量(intensive parameters)则被定义为广延量对应的共轭变量。
特性函数
基本方程$U = U(S,V)$是不好求的,因为它以熵$S$为独立变量,我们没法在实验中直接“测”得熵。好在我们知道,$S, T$是一对共轭变量,理论上可以通过勒让德变换把$U = U(S,V)$的信息转换到对偶空间4$(T, V)$。转换之后的函数形式必然发生一些变化,不过包含的信息是完全一致的。变换方式简单到爆炸:$F(T, V) = U - TS$,恭喜你找到了亥姆霍兹自由能。
有时候体积不好测,能不能转换到$(T, p)$空间呢?恭喜你找到了吉布斯自由能:$G(T, p) = U - TS + pV$。还剩一种变换到$(S,p)$空间的函数也就呼之欲出啦:恭喜你找到了焓:$H(S, p) = U + pV$。所以$U, H, F, G$本质上是一回事,都是内能表象下的基本方程,一旦其自然变量确定下来,全部的热力学信息也就确定了。这四个特性函数都遵循最小值原理。
需要强调的是,上述的符号比如$F(T, V)$说明T和V是亥姆霍兹自由能F的自然变量。F当然可以选择其他参数作为独立变量,比如你一定可以写出一个$F(p, V)$,但是这并非基本方程,不包含全部的热力学信息5。
热容量与Maxwell关系
我们还剩$C_V, C_p$没有说。这一堆实验量$ C_V, C_p, \kappa, \alpha, \beta$其实是基本方程的二阶导数6。如果你的热学老师嗑嗨了,他可能会跟你介绍过Maxwell关系。诸如$\left(\frac{\partial S}{\partial V}\right)_T = \left(\frac{\partial p}{\partial T}\right)_V$这样惨绝人寰的式子,一共有四个,算上他们的倒数有tm八个。他们的本质是基本方程二阶导数的“羁绊”7。别被吓到,它们的关系异常明了:
Maxwell关系能快速化简式子。比如说我们现在想求$U = U(T, V)$的全微分,注意此处的$(T, V)$不是自然变量。$ dU = TdS - pdV $,只要形式上写出$dS(T, V)$即可完成变量的转换。
\[\begin{align} dS(T, V) & = \left(\frac{\partial S}{\partial T}\right)_V dT + \left(\frac{\partial S}{\partial V}\right)_T dV \\[1em] dU(T, V) & = T\left[\left(\frac{\partial S}{\partial T}\right)_V dT + \left(\frac{\partial S}{\partial V}\right)_T dV\right] - pdV \\[1em] & = T\left(\frac{\partial S}{\partial T}\right)_V dT + \left[T \left(\frac{\partial S}{\partial V}\right)_T - p\right] dV \end{align}\]这个时候就该Maxwell关系上场了,看到(3)的第二项中的$\left(\frac{\partial S}{\partial V}\right)_T$,显然可以通过Maxwell关系转化:
\[\begin{equation} \left(\frac{\partial S}{\partial V}\right)_T = \left(\frac{\partial p}{\partial T}\right)_V \end{equation}\]于是:
\[\begin{equation} dU(T,V) = C_V dT + \left[T \left(\frac{\partial p}{\partial T}\right)_V - p\right] dV \end{equation}\]上式利用了$C_V = \left(\frac{\partial U}{\partial T}\right)_V$。
后续我们将通过Maxwell关系推导出非常多有用的公式。尤其是$C_V, C_p$之间的关系:
\[\begin{align} C_p - C_V & = T \left(\frac{\partial V}{\partial T}\right)_p \left(\frac{\partial p}{\partial T}\right)_V \\[1em] & = \frac{TV \alpha^2}{\kappa} \end{align}\]统计物理
热力学最大的问题在于过于依赖实验。物态方程必须通过实验测得,这样非常粗糙。气体系统由微观粒子构成,统计力学将会回答如何将微观量与宏观量联系起来。一个小目标是将物态方程从纯粹的理论中推导出来。
面对粒子数达$10^{23}$数量级的宏观系统,写出每一个粒子的方程然后求解是不可能的。因此,了解统计物理对微观状态的描述异常重要。主要分为认为粒子可分辨的经典描述,和认为微观粒子具有全同性因而不可分别的量子描述。这是第一个层面。
第二个层面是基于等概率原理的统计方法,按照历史的发展分为两套理论。先是玻尔兹曼提出的最概然统计法,即认为宏观系统的平衡态拥有最多的微观状态数。最概然统计法可以成功推导出理想气体,但它有一个致命缺陷:最概然统计法假定粒子之间的相互作用非常弱,可以忽略不计,从而可将系统总能量$E = \sum_i \varepsilon_i+ \sum_{i \neq j} \varepsilon_{ij}$的后一项省略掉。但是,诸如范德瓦尔斯系统是必须考虑粒子相互作用的,后来吉布斯建立系综理论解决了这一问题。系综理论认为一切宏观量是微观量在各态的平均,有点像量子力学中的“力学量用算符表示”:$\langle F \rangle = \langle\phi \vert \hat{F} \vert \phi \rangle$。系综理论还可以解决与大热源和大粒子源接触的开放系统,不再局限于孤立系。
微观运动的描述
对单一组份的气体,经典描述认为所有粒子都长一个样,但是粒子可以被编号。$(1,2)$和$(2,1)$是不一样的。
量子描述认为微观粒子具有全同性,你只能说此刻系统有两个粒子,一个在$r_1$处,另一个在$r_2$处。你不能说”第一个粒子在$r_1$处,第二个粒子在$r_2$处,这是做不到的。因此对于处在两个位置的全同粒子,只贡献一个微观态$(\cdot, \cdot)$
最概然统计法
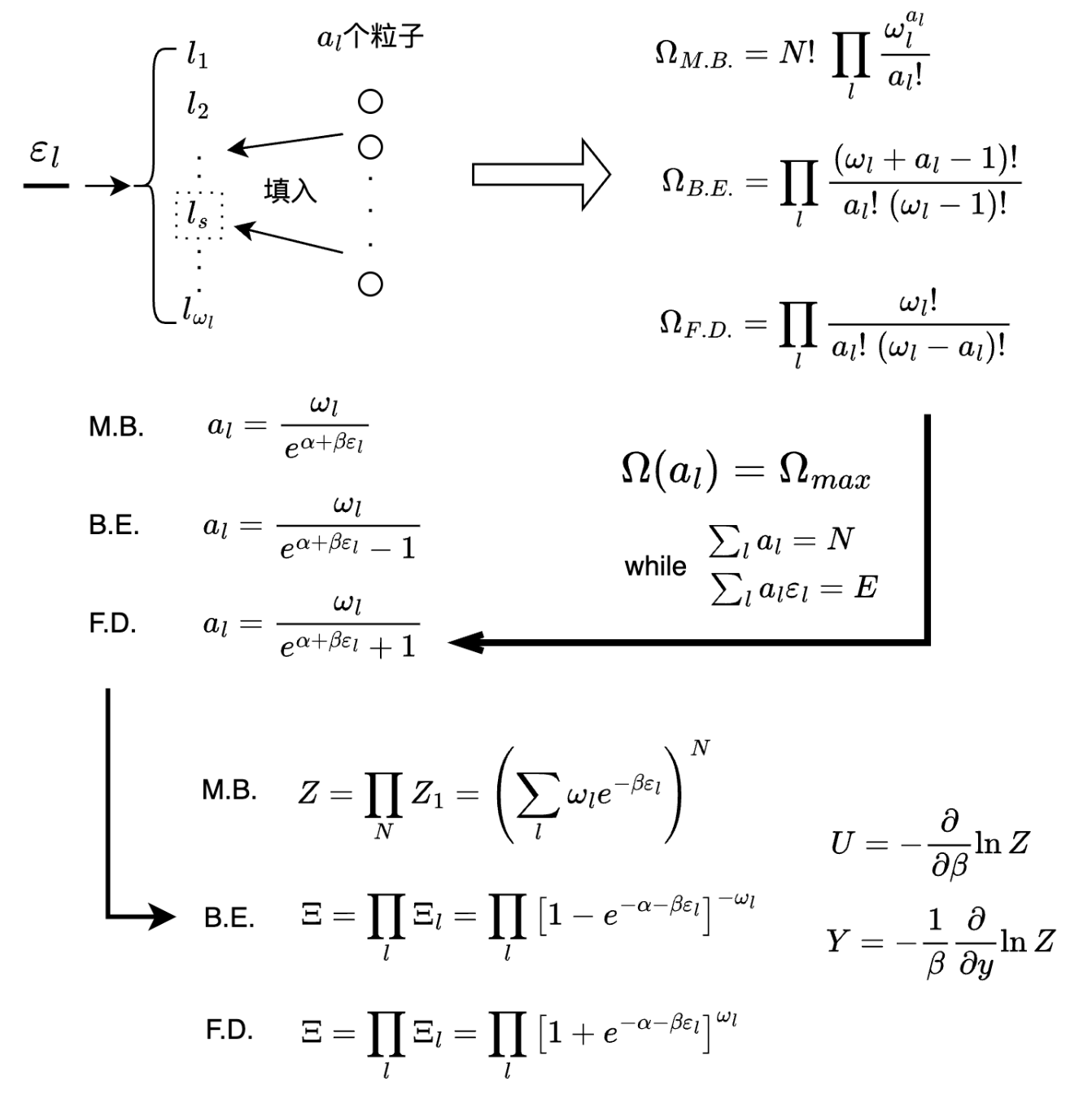
朋友,理解了这张图的左上角,你就理解了最概然统计法的一切。最概然统计法通过粒子分布描述微观状态,即,每一个能级$\varepsilon_l$上,有多少个粒子数$a_l$。你的第一阶段目标就是求出这个$a_l$。
有$\omega_l$个简并度的能级$\varepsilon_l$,将$a_l$个粒子填进去,有多少种不同的填法,就是一个能级下的微观状态数。将每一个能级的微观状态数乘起来,得到系统的微观状态数。这张图的左上角还标注了一个$l_s$,这个$l_s$对应一个量子态。前面我们都是按能级求和,有时候也会按量子态求和,注意随机应变哦。
粒子的分布中包含两个参数$\alpha, \beta$,他们来源于两个约束条件$\sum_l a_l = N, \sum_l a_l \varepsilon_l = E$。不过这两个参数都可解出来,详见下一小节。
经典统计与量子统计
经典统计与量子统计的分界线在于经典极限条件(也叫非简并性条件)$e^{\alpha}\gg1$。从三个分布的$a_l$可以看出来,如果满足经典极限条件,则三者的微观粒子数分布都相同,在此条件下$\Omega$有:
\[\begin{equation} \frac{\Omega_{M.B.}}{N!} \approx \Omega_{B.E.} \approx \Omega_{F.D. } \end{equation}\]这是非常舒服的,因为本来$\Omega_{M.B. }$比别人多了一个$N!$就是因为考虑到粒子可分辨,交换任意两个粒子的位置贡献一种新的微观态。(8)的含义是在经典极限下,大家的行为都是全同粒子😃。
如前所述,$\alpha, \beta$作为拉格朗日乘子法的待定系数,只需要待会约束方程中即可解得。在经典统计下,$\alpha, \beta$分别为:
\[\begin{equation} e^\alpha = \frac{V}{N} \left(\frac{2 \pi m k_B T}{h^2}\right)^{3/2} \qquad \beta = \frac{1}{k_B T} \end{equation}\]在量子统计下,$\alpha, \beta$分别为:
\[\begin{equation} \alpha = - \frac{\mu}{k_B T} \qquad \beta = \frac{1}{k_B T} \end{equation}\]相格与态密度
在图2_最概然统计法_的最下方,是统计力学的精髓:配分函数。不仅是最概然统计法,包括系综理论,都被归结为根据系统求配分函数,按照配分函数求热力学量的范式。此处有个问题:对于经典系统,简并度$\omega_l$指的是什么???
我们如何确定一个自由粒子的状态?只需要给出粒子的位置和动量即可,这对应$\mu$空间中的一个点。粒子可以在等能面上运动,一个面上有无数个点啊!难道说我们要认为一个粒子有无数个状态吗?这是一个很大的矛盾。但我们知道,这个世界上没有什么东西是无限可分的,我们有一个最小尺度,即普朗克尺度。最终这个矛盾是这样解决的8:划分相格,认为一个小相格对应一个态。相格的大小为$d^{3N}q \; d^{3N}p = h_0^{3N}$,此处的$h_0$越小就越精确。$d^{3N}q $为简记,表示其中有$3N$个关于位置的分量。于是经典情况下,简并度和配分函数变为:
\[\begin{align} & \omega_l = \frac{\int d^{3N}q \; d^{3N}p}{h_0^{3N}} \\[1em] & Z_1 = \sum_l \omega_l e^{-\beta \varepsilon_l} = \frac{1}{h_0^3}\int e^{-\beta \varepsilon_l}d^3q \; d^3 p \end{align}\]对于量子系统,我们用态密度来表示单粒子的简并度,其实也是在化相格: \(\begin{equation} \omega_l = D(\varepsilon) = g \frac{V}{(2 \pi)^3}\int_{\text{等能面}}\frac{ds}{\nabla_k\varepsilon(k)} \end{equation}\)
其中g表示自旋所带来的简并。可以看到上述两种做法将求和变成了积分,方便了我们的操作。其背后的原因是$h_0$非常非常小,几乎就是积分了。但是,我们将在玻色-爱因斯坦凝聚章节看到这样做的弊端——积分扔掉了最低能级上的粒子贡献,这在极低温粒子都在最低能级的情况下显然会带来很大问题的。
系综理论
系综理论认为宏观量是微观量在各个态上的平均值: \(\begin{equation} \langle B \rangle = \sum_s \rho_s B_s \end{equation}\) 系统处在s态上的概率$\rho_s$是系综理论的出发点。在对概率密度$\rho_s$作归一化时,配分函数竟然自然而然的出现了,这是很炫酷的事情。对于孤立系统,即$E,N,V$为定值,我们采用微正则系综,$\rho = \frac{1}{\Omega}$;
正则系统处理与大热源接触的系统,即$T, N, V$为定值,此时可以证明$\rho_s \propto e^{-\beta \varepsilon_s}$。显然
\[\begin{equation} \rho_s = \frac{e^{-\beta \varepsilon_s}}{\sum_s e^{-\beta \varepsilon_s}} = \frac{e^{-\beta \varepsilon_s}}{Z} \end{equation}\]巨正则系统处理与大热源和粒子源都接触的系统,即$T,\mu, V$为定值,$\rho_s \propto e^{-\alpha N -\beta \varepsilon_s}$。显然 \(\begin{equation} \rho_{Ns} = \frac{e^{-\alpha N -\beta \varepsilon_s}}{\sum_{N = 0}^{\infty}\sum_se^{-\alpha N -\beta \varepsilon_s}} = \frac{e^{-\alpha N -\beta \varepsilon_s}}{\Xi} \end{equation}\) 可以证明,配分函数与热力学量的关系不变。太好啦!又到了我们最喜欢的求配分函数,再以配分函数为桥梁求热力学量的套路上来啦!