概率论Cheatsheet

分布律

离散型随机变量

二项分布

X服从参数为$n,p$的二项分布：

\[P(X = k) = C_n^k \; p^k(1-p)^{n-k}\]

泊松分布

X服从参数为$\lambda$的柏松分布，其中$\lambda > 0$为参数：

\[P(X = k) = \frac{\lambda^k e^{-\lambda}}{k!} \; , k = 0,1,2,\cdots ,\]

泊松定理

泊松定理

二项分布在n非常大时逼近泊松分布，可以用泊松分布近似计算： $$ \lim_{n \to \infty} C_n^k \; p^k(1-p)^{n-k} = \frac{\lambda^k e^{-\lambda}}{k!} $$ 其中$\lambda = np$。

连续性随机变量

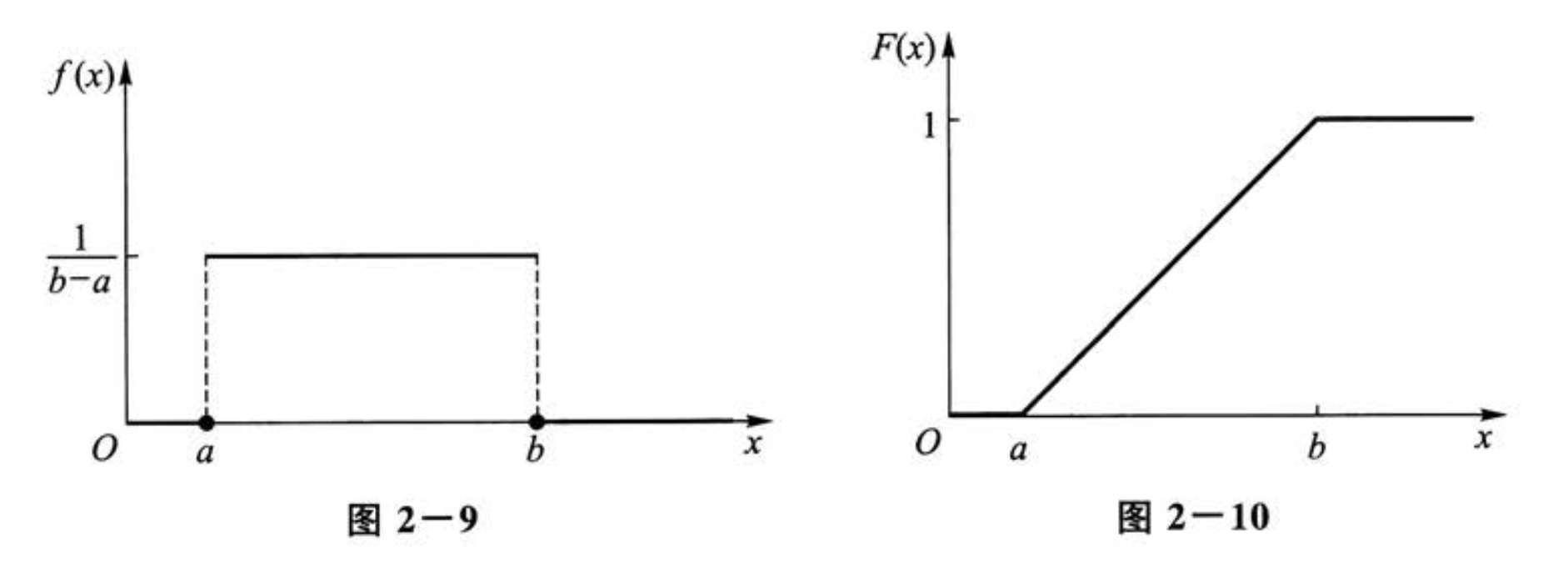
均匀分布

图1. 均匀分布图像

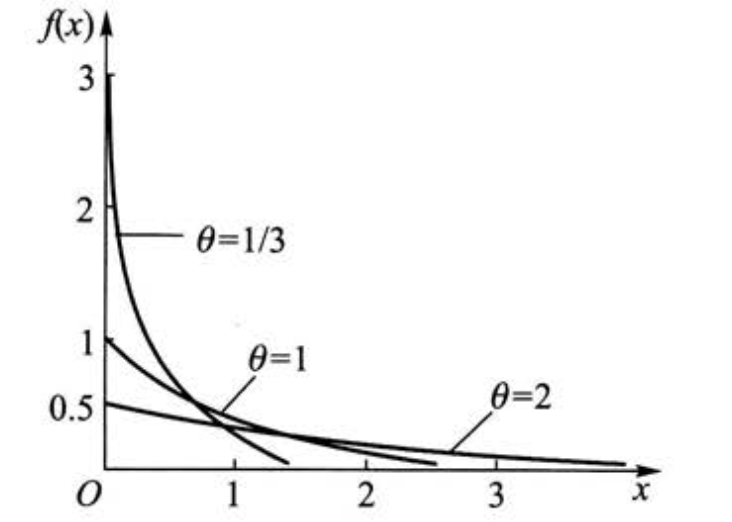
指数分布

\[f(x) = \left\{\begin{aligned} & \frac{1}{\theta} e^{-x/\theta} , \quad x > 0 \\[10pt] & 0, \quad \text{otherwise} \end{aligned}\right.\]

图2. 指数分布图像

正态分布

\[f(x) = \frac{1}{\sqrt{2\pi}\sigma} e^{- \frac{(x - \mu)^2}{2\sigma^2}}, \quad -\infty < x < \infty\]

正态分布标准化

若随机变量$X ~ N(\mu, \sigma^2)$，则$Z = \frac{X-\mu}{\sigma} ~ N(0,1)$